In the previous post “Linear Programming with R” we examined the approach to solve general linear programming problems with “Rglpk” and “lpSolve” packages. Today, let’s explore “lpSolve” package in depth with two specific problems of linear programming: transportation and assignment.
1. Transportation problem

Usage:
lp.transport(cost.mat, direction="min", row.signs, row.rhs, col.signs,
col.rhs, presolve=0, compute.sens=0, integers = 1:(nc*nr))
Code & Output:
#
# Transportation problem, Frederick & Mark (2014, p.95)
#
# Load "lpSolve" package
library(lpSolve)
# Set up cost matrix
costs <- matrix(c(700, 800, 900, 900, 800, 700), nrow = 2)
# Set up constraint signs and right-hand sides
row.signs <- rep("<=", 2)
row.rhs <- c(12, 15)
col.signs <- rep(">=", 3)
col.rhs <- c(10, 8, 9)
# Run
lptrans <- lp.transport(costs, "min", row.signs, row.rhs, col.signs, col.rhs)
lptrans$solution
[,1] [,2] [,3]
[1,] 10 2 0
[2,] 0 6 9
lptrans$objval
[1] 20500
The solution is shown as lptrans$solution and the total cost is 20500 as lptrans$objval.
2. Assignment problem
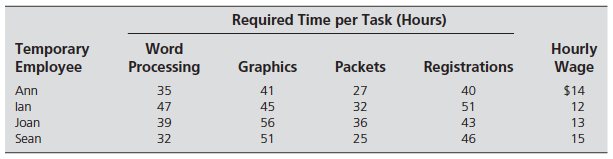
Usage:
lp.assign(cost.mat, direction = "min", presolve = 0, compute.sens = 0)
Code & Output:
#
# Assignment problem, Frederick & Mark (2014, p.99)
#
# Load "lpSolve" package
library(lpSolve)
# Set up cost matrix
a <- matrix(c(35, 41, 27, 40, 47, 45, 32, 51, 39, 56, 36, 43, 32, 51, 25, 46), nrow = 4, byrow = TRUE)
b <- c(14, 12, 13, 15)
cost.mat <- a*b
# Run
lpassign <- lp.assign(cost.mat, direction = "min")
lpassign$solution
[,1] [,2] [,3] [,4]
[1,] 0 0 1 0
[2,] 0 1 0 0
[3,] 0 0 0 1
[4,] 1 0 0 0
lpassign$objval
[1] 1957
Similarly, the solution and the total cost are shown as lpassign$solution and lpassign$objval respectively.
This article was really helpful, but I am facing issue while solving unbalanced transportation problem when there is excess demand. Could you please guide me on what has to be done in this case.
Hello sir, this article was really helpful. But, I am facing issue while solving unbalanced transportation problem when there is excess demand, it gives solution as no feasible solution. works perfectly fine for balanced and excess supply problems. Could you please guide me on why this issue is occurring and a possible solution for the same.
Thank you.