After finished the Business Statistics course in my Pre-Master at Nyenrode, I felt myself comfortable to deal with data analysis, and I did not have big plans for the six-week winter holiday, so I was wondering maybe I could try some different things about data analytics. However, since I am not a fan of drag-and-drop tools such as Excel and SPSS, I ended up with R, which many friends have recommended before.
Meanwhile, I realized that there will be a course about Operation Research called “Introduction to Management Science: A Modeling and Cases Studies Approach with Spreadsheets“, which is about how to solve Operation Research questions with excel Modeling, so I began to looking for R packages for Operation Research.
In this post, I will demonstrate how to use R to solve a Linear Programming question in the book with two different packages: “Rglpk” and “lpSolve”.
2.1 A CASE STUDY: THE WYNDOR GLASS CO. PRODUCT-MIX PROBLEM

Rglpk usage:
Rglpk_solve_LP(obj, mat, dir, rhs, bounds = NULL, types = NULL, max = FALSE, control = list(), …)
Rglpk code & output:
# Loading package of "Rglpk"
library(Rglpk)
# Vector of objective coefficients
obj <- c(300, 500)
# Matrix of constraint coefficients
mat <- matrix(c(1, 0, 0, 2, 3, 2), nrow = 3, ncol = 2, byrow = TRUE)
# Vector with the directions of the constraints
dir <- c("<=", "<=", "<=")
# Vector representing the right-hand side of the constraints
rhs <- c(4, 12, 18)
lp1 <- Rglpk_solve_LP(obj, mat, dir, rhs, types = "I", max = TRUE)
lp1
$optimum
[1] 3600
$solution
[1] 2 6
$status
[1] 0
$solution_dual
[1] NA
$auxiliary
$auxiliary$primal
[1] 2 12 18
$auxiliary$dual
[1] NA
As the output shows that the best solution is to produce 2 doors and 6 windows and the total profit would be 3600.
Similarly, lpSolve code & output is like this:
# Loading package of "lpSolve"
library(lpSolve)
lp2 <- lp(direction = "max", objective.in = c(300, 500), const.mat = matrix(c(1, 0, 0, 2, 3, 2), nrow = 3, ncol = 2, byrow = TRUE), const.dir = c("<=", "<=", "<="), const.rhs = c(4, 12, 18))
lp2$solution
[1] 2 6
lp2$objval
[1] 3600
One of the advantages of R compared to other drag-and-drop tools is that we can reuse the code for all the similar questions. Learning R is paying off now 🙂
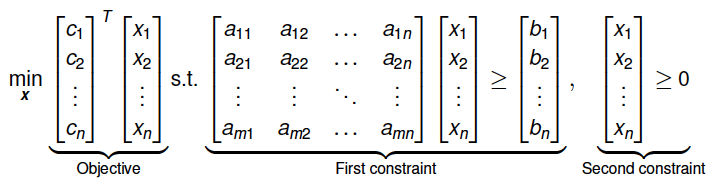
Hi Henry, there’s an error in the figure. The constraint RHS b should be b_m not b_n!